Οι κίνδυνοι στα Δικαιώματα Προαίρεσης
Ολα όσα πρέπει να γνωρίζουν οι επενδυτές. Τα γκρίζα σημεία και οι παγίδες.

Μιλώντας για Δικαιώματα Προαίρεσης (ΔΙΠ), αυτά χαρακτηρίζονται από μία πολύπλοκη αφήγηση, η οποία αποσαφηνίζεται ιδιαίτερα με τη διάκριση δύο κριτηρίων επί της τιμής: το κριτήριο αναφοράς και το κριτήριο σχέσης. Στο παρόν άρθρο, θα δούμε κάποια «γκρίζα σημεία» στην ανάλυση του πολυσχιδούς αυτού επενδυτικού οχήματος.
» Δύο κριτήρια τιμής
Από τη μία, το κριτήριο αναφοράς αφορά σε τρεις τιμές, την «πρώτη» τιμή (την τιμή της υποκείμενης από την οποία «παράγεται» το ΔΙΠ), τη «δευτέρα» τιμή (την τιμή εξάσκησης του ΔΙΠ στη λήξη, δηλαδή το strike) και την «τρίτη» τιμή (την τιμή του ΔΙΠ στο ταμπλό, δηλαδή το premium). To σημαντικότερο σημείο είναι ότι η «τρίτη» τιμή εξαρτάται μεν από τις άλλες δύο (1), αλλά μόνο αυτή αντιπροσωπεύει την πραγματική ονομαστική αξία του ΔΙΠ, διότι μόνο εκείνη εμπλέκεται στον υπολογισμό της αξίας της συναλλαγής. Από την άλλη, το κριτήριο της σχέσης αφορά αποκλειστικά στον τρόπο με τον οποίο μεταβάλλεται η «τρίτη» τιμή σε σχέση με την «πρώτη» τιμή.
Ειδικότερα, η τρέχουσα αξία ενός ΔΙΠ έως τη λήξη εξαρτάται από την εσωτερική και τη χρονική αξία, αλλά ο τρόπος με τον οποίο μεταβάλλονται αυτές είναι μοναδικός και εντελώς διαφορετικός από τον τρόπο υπολογισμού των υπολοίπων επενδυτικών οχημάτων, όπως πχ των ΣΜΕ: επί παραδείγματι, η μεταβολή +10% της τιμής της υποκείμενης -ας πούμε, μετοχής- θα μεταβάλλει σχεδόν (2) +10% την τιμή του ΣΜΕ της, αλλά θα μεταβάλλει ίσως +10%, +150%,-50% την τιμή του ΔΙΠ της.
Η αλήθεια είναι ότι απαιτείται μία μικρή εξοικείωση στα ΔΙΠ, υπό δύο συσχετιζόμενες μεταξύ τους έννοιες: πρώτον, η εξοικείωση με την κατεύθυνση αυτών είναι βασικότατη, καθώς είναι γνωστό ότι υπάρχουν τέσσερα «κλαδιά» ως βασικές θέσεις, το long CALL και το short PUT, η τιμή των οποίων χονδρικά εκφέρεται ως θετικά συσχετισμένη με την κίνηση της τιμής της υποκείμενης, και το long PUT και short CALL, η τιμή των οποίων εκφέρεται αντίστοιχα αρνητικά συσχετισμένη με την κίνηση της τιμής της υποκείμενης. Δεύτερον, η ποιότητα της κίνησης του εκάστοτε «κλαδιού» αφορά σε ένα μοντέλο θεωρητικής αποτίμησης, στο οποίο εισάγονται πολλαπλασιαστικά ή υποπολλαπλασιαστικά κάποιες μεταβλητές ώστε να επηρεάσουν την τελική «τρίτη» τιμή των ΔΙΠ.
Το σημείο-κλειδί των short θέσεων
Σχετικά με κάποια γνωστά βασικά χαρακτηριστικά των long θέσεων σε CALL και PUT, ένα εξ αυτών είναι το περιορισμένο και προκαθορισμένο ύψος ζημίας σε περίπτωση έντονης αρνητικής (ως προς την πρόβλεψη) κίνησης της τιμής της υποκείμενης. Το μέγεθος αυτό καθορίζεται από το ύψος του premium, της «πρώτης» τιμής δηλαδή που θα αγορασθεί το long CALL ή PUT στο ταμπλό την ώρα της συναλλαγής, και αφορά έως και στο 100% αυτού, χωρίς να ενδιαφερόμεθα πλέον για την έντονη αρνητική -ως προς την πρόβλεψη- κίνηση της τιμής της υποκείμενης. Εν αντιστοιχία, το χαρακτηριστικό των short θέσεων σε αυτήν την ιδιαιτερότητα είναι το περιορισμένο και προκαθορισμένο κέρδος (η ζημία για τα long είναι το κέρδος για τα short), το οποίο αφορά στο απολεσθέν premium των long θέσεων, ενώ η ζημία είναι θεωρητικά απεριόριστη.
Κι όμως, θα περίμενε κάποιος με αυτά τα δεδομένα να προτιμώνται οι long θέσεις, καθώς δίνουν στο συναλλασσόμενο τα ονειρεμένα στοιχεία: μικρή ζημία και απεριόριστο κέρδος. Από την άλλη, η απεριόριστη ενδεχόμενη ζημία για τις short θέσεις και το περιορισμένο μικρό κέρδος δίδει την αίσθηση ότι ο πωλητής των ΔΙΠ είναι λάτρης του κινδύνου, διότι αναλαμβάνει μία θέση στην οποία βρίσκεται πέρα για πέρα εκτεθειμένος.
Τα πράγματα όμως ενέχουν έναν άλλο παράγοντα, ο οποίος έρχεται πάντα να επιβεβαιώνει τη ρήση «τίποτα δεν είναι δωρεάν»: το φαινομενικά «υψηλό» ρίσκο που αναλαμβάνουν οι short θέσεις εξηγείται πολύ απλά από την υπεροχή τους στη μικρή πιθανότητα που υπάρχει να το αντιμετωπίσουν στην πραγματικότητα. Η επεξήγηση αυτού προέρχεται από την εμπεριστατωμένη ανάλυση της πιθανοτικής κατανομής, στην οποία δε θα επιμείνουμε μεν, αλλά θα βασισθούμε σε αυτήν για να εξηγήσουμε με απλά λόγια τί πραγματικά συμβαίνει. Η πολυπλοκότητα που διέπει τέτοιου είδους προσέγγιση δε μάς επιτρέπει να εξηγήσουμε με μαθηματική ορολογία, καθώς δεν αφορά στο χαρακτήρα του άρθρου. Όμως, κάθε προσέγγιση μη περιλαμβάνουσα την έννοια της πιθανότητας θα ήταν το λιγότερο ελλιπής, άσχετα εάν στην καθημερινή τριβή με τις χρηματαγορές συνηθίζεται να ακολουθείται κάποιο αυτοματοποιημένο μοτίβο που διευκολύνει τους υπολογισμούς.
Χιλιομετρικές αποστάσεις
Γενικά, ο επενδυτής αποφασίζει να εμπλακεί σε μια οποιαδήποτε συναλλαγή σκεπτόμενος εάν η πιθανότητα να αποδώσει η επένδυση είναι μεγαλύτερη από την πιθανότητα να μην αποδώσει, και εάν το κέρδος του από μία επιτυχημένη επένδυση είναι μεγαλύτερο από τη ζημία του σε μία αποτυχημένη επένδυση, σε σχετικούς πάντα όρους. Αυτό φαίνεται μεν αυτονόητο, αλλά εμπεριέχει μέσα μία βαθύτερη προσέγγιση. Ας το σκεφθούμε διαφορετικά: όταν αγοράζει κάποιος μία μετοχή, έχει πιθανότητα 50% να δει την τιμή της να ανεβαίνει και 50% να πέφτει, εξαίροντας εδώ για λόγους απλούστευσης πιθανές πληροφορίες ή περαιτέρω πιθανοτική πρόβλεψη.
Ας φαντασθούμε λοιπόν ότι ο επενδυτής είναι στο μέσο ενός ευθύγραμμου τμήματος˙ αριστερά του, είναι το «κάτω» της τιμής της μετοχής, δεξιά του, είναι το «πάνω». Τα άκρα του ευθύγραμμου τμήματος είναι πάρα πολύ μακριά, και τα οποία παρομοιάζουν την απόσταση της τιμής-στόχου από την τιμή της υποκείμενης τη στιγμή της συναλλαγής: εάν μία μετοχή έχει στο ταμπλό 1€, το δεξί άκρο φθάνει έως το -θεωρητικά- άπειρο, το αριστερό άκρο φθάνει ως το -θεωρητικά- μηδέν, και η απόσταση αυτή είναι πάρα πολύ μακρινή να καλυφθή σε όρους πιθανοτήτων.
Διότι είναι σχεδόν απίθανο η τιμή να φθάσει στο άπειρο ή στο μηδέν στιγμιαία, ή εν πάσει περιπτώσει σε εύλογο χρονικό διάστημα (το οποίο στην ανάλυση των ΔΙΠ καθορίζεται από το χρόνο λήξης του εκάστοτε ΔΙΠ).
Έτσι λοιπόν, με την τιμή της μετοχής στο 1€, έχουμε να αντιμετωπίσουμε τα εξής: η κίνηση της τιμής προς τα 0.90€ έχει περίπου πιθανότητα 34% να συμβεί, ομοίως και η κίνηση προς τα 1.10€. Αντίστοιχα, η κίνηση της τιμής προς τα 0.80€ έχει πιθανότητα 13% να συμβεί, ομοίως και η κίνηση προς τα 1.20€. Η κίνηση προς τα 0.70€ ή τα 1.30€ είναι αρκετά δύσκολη, ας πούμε με πιθανότητα 2%. Τέλος, κάτω από τα 0.70€ ή πάνω από τα 1.30€ η πιθανότητα είναι ελάχιστη έως και αμελητέα.
Η παραπάνω αφήγηση εξηγεί παιδικά την έννοια της τυπικής κανονικής κατανομής, θεωρώντας εντελώς άστοχα ότι ο μέσος όρος την τρέχουσα στιγμή είναι το 1€ και η τυπική απόκλιση 0.10€, πάντα με δεδομένες συνθήκες της αγοράς. Πάντως, άσχετα με τη θεωρητική προσέγγιση, η κατανομή αυτή των πιθανοτήτων στην κίνηση της τιμής της μετοχής του 1€ δεν είναι και άσχημη σε τελική ανάλυση, και θα τη δεχθούμε προς το παρόν για να συνεχίσουμε το σκεπτικό μας. Διότι πολύ απλά, σκεφθείτε πόσες φορές έχετε δει μία μετοχή με πρόσημο ±5%, πόσες φορές με πρόσημο ±10%, πόσες με ±30%, κ.ο.κ. Προφανώς, οι μεγάλες ποσοστιαίες αποκλίσεις εμφανίζονται -ας πούμε- σπάνια, οι μικρές εμφανίζονται -ας πούμε- συχνά (3).
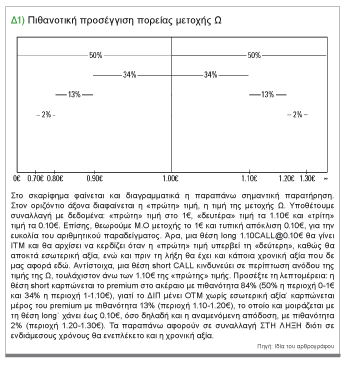
Ό,τι ανεβαίνει, κατεβαίνει
Προσέξτε δύο λεπτομέρειες: α) όσο μεγαλώνει ο κίνδυνος, ο οποίος σε απόλυτους όρους εκφέρεται ως ένα μεγάλο ποσοστό αρνητικής -ως προς την πρόβλεψη- μεταβολής, τόσο μειώνεται η πιθανότητα να πραγματοποιηθεί: εάν κάποιος ηγόραζε με 1€ τη μετοχή, έχει μία «μεγάλη» πιθανότητα (34%) να χάσει 0.10€˙ έχει «μικρότερη» πιθανότητα (13%) να χάσει περισσότερα (0.20€)˙ έχει ακόμα «μικρότερη» πιθανότητα (2%) να χάσει ακόμα περισσότερα (0.30€), κ.ο.κ. Τί παρατηρείτε σε πρώτη ανάγνωση; «..έχει μικρότερη...να χάσει περισσότερα..», «έχει ακόμα μικρότερη...να χάσει ακόμα περισσότερα..». Αυτό επιβεβαιώνει και την πεποίθηση ότι η αγορά τείνει να αποτιμά τα πάντα, καθώς οι μεγάλες αποδόσεις ενέχουν και μεγάλο ρίσκο.
Το ίδιο ισχύει και από την αντίθετη πλευρά, αυτήν του κέρδους: όσο μεγαλώνει η απόδοση, τόσο μικραίνει και η πιθανότητα να εμφανισθή τέτοια. Κι αυτό διότι η παραπάνω επεξήγηση για το τί πάει να χάσει ο επενδυτής σε όρους πιθανοτήτων ισχύει και για το τί πάει να κερδίσει: έχει πιθανότητα 34% να κερδίσει 0.10€, πιθανότητα 13% να κερδίσει 0.20€, κτλ. Δηλαδή, έχει «μεγάλη» πιθανότητα να κερδίσει «μικρό» ποσό, «μεγαλύτερη» πιθανότητα να κερδίσει «μικρότερο» ποσό, κ.ο.κ. Και το αστείο είναι ότι είτε η μετοχή είχε 1€ και υπολογίζαμε ±0.10€, ±0.20€ κ.ο.κ, είτε είχε 2€ και υπολογίζαμε ±0.20€, ±0.40€ δε θα άλλαζε κάτι. Όλα είναι θέμα μεταβολών, δηλαδή ποσοστών.
β) αναφερόμεθα στη «ζώνη υποδοχής» των 1.10€, 1.20€, 1.30€ και αντίστοιχα 0.90€, 0.80€, 0.70€, χωρίς να καθορίζομε το χρόνο. Αυτό έρχεται και σε άμεση συσχέτιση με την ανάλυση του ΤΗΕΤΑ, καθώς όσο μεγαλύτερος ο χρόνος, τόσο καλύτερες οι πιθανότητες να κινηθή η τιμή 10% (στα 0.90€ ή 1.10€), κάτι που με τη σειρά του θα αυξομείωνε το εύρος κίνησης. Διότι είναι διαφορετικό να απαντήσουμε στο «ποία η πιθανότητα να κινηθεί +10% η μετοχή Ω σε μία μέρα», από το να απαντήσουμε στο «ποία η πιθανότητα να κινηθεί +10% η μετοχή Ω σε ένα μήνα». Κι όμως, με δεδομένα επίπεδα πιθανοτήτων (34%, 13%, 2%) θα πρέπει να αναπροσαρμόζομε αντίστοιχα το εύρος κίνησης, απαντώντας τελικά σε διαφορετικές ερωτήσεις, όπως «πού θα πάει αύριο η μετοχή Ω στο 34% των περιπτώσεων», «πού θα πάει στο 13% των περιπτώσεων», κτλ.
Αντίστοιχα με την πιθανοτική κατανομή ως προς την τιμή της μετοχής εκφράζουμε και την πρόβλεψή μας για την τιμή των ΔΙΠ. Θυμηθείτε ότι η «τρίτη» τιμή των ΔΙΠ αποτιμάται βάσει της τιμής της υποκείμενης μετοχής, εμπλέκοντας και κάποιες μεταβλητές που εδώ δε μας αφορούν. Άρα, η ανάλυση της κίνησης της τιμής της υποκείμενης επηρεάζει και την απόφασή μας για τη συναλλαγή σε ΔΙΠ. Συγκεντρώνοντας λίγο την παραπάνω προσέγγιση, θα πούμε με απλά λόγια εάν η μετοχή έχει πιθανότητα 34% να κινηθεί ανοδικά κατά 10% (στο απλοϊκό παράδειγμά μας), η πιθανότητα να κινηθεί 10% η τιμή ενός ΔΙΠ ΙΤΜ είναι διαφορετική, η πιθανότητα να κινηθεί 10% η τιμή ενός ΔΙΠ ΟΤΜ είναι διαφορετική, διαφορετική επίσης για ένα ΔΙΠ λήξης μιας εβδομάδας, δύο εβδομάδων, για ένα ΔΙΠ strike 1.10€, 1.20€, κ.ο.κ. Άρα, τα ΔΙΠ, η τιμή των οποίων έχει πιθανότητα 34% να κινηθεί υπέρ μας, είναι διάφορα αυτών που έχουν πιθανότητα 13% να κινηθούν προς αυτήν, κ.ο.κ. Και φυσιολογικά, χωρίς να απαιτείται να υπεισέλθουμε σε μαθηματικές λεπτομέρειες, όσο μικραίνει αυτή η πιθανότητα, τόσο μεγαλώνει και το ενδεχόμενο κέρδος.
Αντίστοιχα, όσο μικραίνει το μέγεθος της ενδεχόμενης ζημίας (στις long θέσεις) τόσο μεγαλώνει και η πιθανότητα να πραγματοποιηθεί η εν λόγω ζημία. Σκεφθείτε το λογικά: εάν η πιθανότητα να συμβεί το κέρδος ήταν θετικά συσχετισμένη με το μέγεθος αυτού, τότε όλοι θα κέρδιζαν μεγάλα ποσά χωρίς ρίσκο. Άρα, για να συναλλασσόμεθα με περιορισμένο ρίσκο (long θέσεις) θα πρέπει αντίστοιχα να δεχόμεθα μεγάλες πιθανότητες να το αντιμετωπίσουμε. Υπενθυμίζουμε δε κατά τα γνωστά ότι το THETA, το οποίο αποτυπώνει τη φθορά του χρόνου, είναι αρνητικό για τις long θέσεις, κάτι που ομοίως επιδρά στην τιμή του: ο αγοραστής των ΔΙΠ, όσο περνάνε οι μέρες, αντιμετωπίζει όλο και μικρότερες πιθανότητες να δει την επένδυσή του να κερδίζει.
Με άλλα λόγια, η χρονική αξία μειώνεται σταδιακά, ενώ η εσωτερική αξία είναι άσχετη με το χρόνο σε απόλυτους όρους (ή θα είναι ΙΤΜ ή δε θα είναι). Επίσης, σχετικά με τη ροή του χρόνου, να σημειώσουμε ότι εάν το ΔΙΠ λήγει σε τριάντα μέρες, μία μέρα συμβολίζει το 1/30 της διάρκειας ζωής του ΔΙΠ, αλλά εάν ένα ΔΙΠ λήγει σε πέντε μέρες, μία μέρα συμβολίζει το 1/5. Τούτο υποδηλώνει ότι μάς ενδιαφέρει επίσης ο ρυθμός μεταβολής του χρόνου, ο οποίος εξαρτάται από την επιλογή της σειράς λήξης του ΔΙΠ.
Αντί επιλόγου
Το άρθρο συνεχίζεται στο επόμενο τεύχος, με μια ενδιαφέρουσα αναφορά σε δύο «κρυφές γωνίες» των Δικαιωμάτων Προαίρεσης: θα δούμε κάποια εναλλακτική προσέγγιση ως προς το breakeven, και θα μετρήσουμε κατά πόσο η «περιορισμένη ζημία» των long θέσεων είναι βάσιμη σημειολογικά.
Το παρόν άρθρο αποτελεί τροποποιημένο απόσπασμα από το σύγγραμμα του ιδίου του συγγραφέα, με τίτλο «Επενδυτική Συλλογιστική», εκδόσεις Φυλάτος 2016. Το εν λόγω σύγγραμμα πραγματεύεται σκόρπιες εμπειρίες επενδυτών και σοβαρά ζητήματα από τη μακροοικονομική και χρηματοοικονομική επιστήμη, παράξοντα μία γενικότερη κερδοφόρο φιλοσοφία γύρω από την ενασχόληση με τις χρηματαγορές. Για τη συγγραφή του, η συνδρομή του υπ. διδάκτoρος του Παν. Πειραιώς Απόστολου Μποζίκα, ήταν σημαντικότατη.
Σημειώσεις
1. Συνολικά, πέντε είναι οι παράγοντες που επιδρούν στη θεωρητική αποτίμηση, 1) η τιμή της υποκείμενης («πρώτη» τιμή), 2) η τιμή εξάσκησης («δεύτερη τιμή»-strike) την οποία επιλέγει ο επενδυτής όταν αγοράζει τα ΔΙΠ βάσει στρατηγικής ή πρόβλεψής του, 3) η λήξη τους (ο χρόνος δηλαδή που απομένει), 4) η μεταβλητότητα της αγοράς και 5) το επιτόκιο.
2. Η διαφορά μπορεί να προέλθει από τον υπολογισμό της «βάσης» ή από διάφορα εταιρικά γεγονότα, όπως ΑΜΚ, διανομή μερίσματος, κλπ.
3. Αν θέλαμε να το δυσκολέψουμε περισσότερο, θα λέγαμε επίσης ότι σε μετοχές με «ιστορικό» μεγάλων μεταβολών, οι μεγάλες μεταβολές εμφανίζονται συχνότερα από ότι σε μετοχές χωρίς τέτοιο «ιστορικό». Αντίθετα, μετοχές που είχαν εμφανίσει «βαριά» συμπεριφορά, τείνουν να συνεχίζουν τέτοια, ώστε να εμφανίζουν συχνότερα μικρότερες ποσοστιαίες διακυμάνσεις από ότι οι «ελαφριές» μετοχές. Αυτή η συμπεριφορά επίσης επεξηγείται με το συντελεστή beta, ο οποίος αποτυπώνει σε γενικές γραμμές και τη μεταβλητότητα της μετοχής. Αυστηρότερα, ο beta αφορά σε ένα μέτρο των μεταβολών της απόδοσης ενός μεγέθους (π.χ τιμή μετοχής) σε σχέση με τις αντίστοιχες ενός μεγέθους αναφοράς (benchmark, π.χ ΓΔ), κύρια χρησιμοποιούμενος σε μοντέλα αποτίμησης τύπου CAPM κλπ, υπολογιζόμενος ως ο λόγος της συνδιακύμανσης της μετοχής με το δείκτη αναφοράς προς τη διακύμανση του δείκτη αναφοράς.
